そのバックテスト本当に再現性ありますか？(その2)

1. 実はかなり難しい金融でのバックテスト

前回、同じデータセットを使ってバックテストを何度も行うと、シャープレシオの真値が0にも拘わらず、シャープレシオの推定値がたまたま2付近に近づくことがありますよ、という話をしました。また、そういった事象を起こりにくくするためには、試行(錯誤)の回数を増加させるにつれてバックテスト期間を延ばす必要があります、という話もしました。

これだけでもバックテストって難しいんですが、よくあるバックテストの誤りとして、こちらでは以下7点が挙げられています。

Survivorship bias(生存者バイアス)
- Using as investment universe the current one, hence ignoring that some companies went bankrupt and securities were delisted along the way.(拙訳：現在のユニバースを投資戦略のユニバースとして使用しているが故に、倒産した企業がいたことや途中で上場廃止になった証券があったことを無視しています。)
Look-ahead bias(先行バイアス)
- Using information that was not public at the moment the simulated decision would have been made. Be certain about the timestamp for each data point. Take into account release dates, distribution delays, and backfill corrections.(拙訳：シミュレーションでの意思決定が行われたその時点では公開されていなかった情報を利用すること。各データポイントのタイムスタンプを確認してください。情報公開日、配布の遅延、差し戻しの修正を考慮に入れる必要があります。)
Storytelling(ストーリーテリング)
- Making up a story ex-post to justify some random pattern.(拙訳：事後的な記事の話をでっち上げて、ランダムなパターンを正当化している。)
Data mining and data snooping(データマイニングとデータスヌーピング)
- Training the model on the testing set.(拙訳：テスト用データセットでモデルを学習すること。)
Transaction costs(取引コスト)
- Simulating transaction costs is hard because the only way to be certain about that cost would have been to interact with the trading book (i.e., to do the actual trade).(拙訳：取引コストをシミュレーションするのは難しいです。なぜなら、そのコストについて確信を持つ唯一の方法は、トレーディングブックと対話することだからです（つまり、実際の取引を行うこと）。)
Outliers(外れ値)
- Basing a strategy on a few extreme outcomes that may never happen again as observed in the past.(拙訳：過去に観察された二度と起こらないかもしれないいくつかの極端な結果に戦略を基づかせること。)
Shorting(空売り)
- Taking a short position on cash products requires finding a lender. The cost of lending and the amount available is generally unknown, and depends on relations, inventory, relative demand, etc.(拙訳：キャッシング商品のショートポジションを取るには、貸し手を探す必要があります。貸出のコストや利用可能な金額は一般的には不明で、関係性、在庫、相対的な需要などに依存します。)

さらに、前回書いたように、非の打ち所がないバックテストを行ったとしても試行錯誤数が多ければ、たまたまシャープレシオが1を超えましたという戦略は1つは出てくることが期待されるわけですからより厄介です。同資料では、再現性のあるバックテストを行うために以下6点が汎用的な手段として挙げられていました。これは前回記事の最後に記載しましたが、再掲します。

Develop models for entire asset classes or investment universes, rather than for specific securities. Investors diversify, hence they do not make mistake X only on security Y. If you find mistake X only on security Y, no matter how apparently profitable, it is likely a false discovery. (拙訳：特定の有価証券ではなく、アセットクラス全体またはユニバース全体のモデルを開発すること。投資家はリスクを分散させているので、彼らはある証券Yだけに対してミスXをすることはありません。あなたが証券YだけにミスXを見つけた場合は、それがどんなに明らかに有益であっても、誤発見である可能性が高い。)
Apply bagging as a means to both prevent overfitting and reduce the variance of the forecasting error. If bagging deteriorates the performance of a strategy, it was likely overfit to a small number of observations or outliers. (拙訳：オーバーフィットを防ぎ、予測誤差の分散を減らすための手段として、バギングを適用すること。バギングが戦略のパフォーマンスを悪化させる場合、それは少数の観測値または外れ値にオーバーフィットした可能性が高い。)
Do not backtest until all your research is complete. (拙訳：すべてのリサーチが完了するまでバックテストをしないこと。)
Record every backtest conducted on a dataset so that the probability of backtest overfitting may be estimated on the final selected result (see Bailey, Borwein, López de Prado and Zhu(2017)), and the Sharpe ratio may be properly deflated by the number of trials carried out (Bailey and López de Prado(2014.b)). (拙訳：研究者が最終的に選択したバックテスト結果がオーバーフィットしている確率を推定できるように、単一の(同じ)データセットで実施されたバックテストをすべて記録すること（Bailey, Borwein, López de Prado and Zhu [2017]）、また、実施された試行数によってシャープレシオを適切にデフレーションできるようにすること（Bailey and López de Prado [2014]）。)
Simulate scenarios rather than history. A standard backtest is a historical simulation, which can be easily overfit. History is just the random path that was realized, and it could have been entirely different. Your strategy should be profitable under a wide range of scenarios, not just the anecdotal historical path. It is harder to overfit the outcome of thousands of “what if” scenarios. (拙訳：ヒストリカルではなくシナリオをシミュレーションすること。標準的なバックテストはヒストリカルシミュレーションであり、オーバーフィットしやすい。歴史(これまでの実績)はランダムなパスの実現値に過ぎず、全く違ったものになっていた可能性があります。あなたの戦略は、逸話的なヒストリカルパスではなく、様々なシナリオの下で利益を得ることができるものであるべきです。何千もの「もしも」のシナリオ結果をオーバーフィットさせるのは(ヒストリカルシミュレーションで過学習するよりも)より難しいことです。)
Do not research under the influence of a backtest. If the backtest fails to identify a profitable strategy, start from scratch. Resist the temptation of reusing those results. (拙訳：バックテストのフィードバックを受けてリサーチしないこと。バックテストが有益な戦略を見つけ出すことに失敗した場合は、ゼロからリサーチを再始動してください。それらの結果を再利用する誘惑に抗ってください。)

いろいろ制約が多すぎて、「じゃあ具体的にどうやってバックテストすればええねん！！」って怒りたくなっちゃいますよね。今回は、著者であるMarcos López de Pradoがお勧めするバックテスト手法である「Combinatorial Purged Cross-Validation」についてレビューしたいと思います。この人、AQR Capital Managementの機械学習部門のトップかつ、 Lawrence Berkeley National Laboratoryのリサーチフェロー & 金融経済学博士 & 数理経済学博士らしいです。バケモンですね。

2. バックテスト手法のいろいろ

一言でバックテスト手法と言っても、やり方はいくつかあります。本節は以下の3つの手法について簡単にレビューし、次節でシミュレーションを行います。

Walk Forward
Cross-Validation
Combinatorial Purged Cross-Validation

2.1 Walk Forward

Wakl Forward(WF)は以下の図のようにテストデータのうち学習データとテストデータの期間をそれぞれ決めておいて、一番最初のデータから学習 & テストを逐次的に繰り返していく手法です(hold-out法を逐次的にしたやつ)。

図1 Walk Forward

WFは、過去に戦略がどのようなパフォーマンスを発揮していたかをヒストリカルにシミュレーションしたものです。各戦略における投資判断は、その判断に以前に確定しているデータに基づいています。

利点
- ストレートフォワードにシミュレーションするのでWFは解釈が明快。
- パージが適切に実装されている限り、末尾のデータを使用することがテストセットがOut-of-Sampleであること（Leakageがない）を保証している。
欠点
- 単一のシナリオがテストされているので、オーバーフィットしやすい(Bailey et al. [2014])。
- WFは、データ点の特異な(再現性のない)挙動によって結果が偏る可能性があるので、必ずしも将来のパフォーマンスを代表するものではない。実際に、WFをオーバーフィットしやすく、観測の順序を変えると一貫性のない結果が得られるという事実事態がオーバーフィッティングしている証拠である。
- 学習初期段階の投資判断は、サンプル全体のごく一部で行われる。ウォームアップ期間が設定されていても、その情報の大部分は投資判断のごく一部でしか利用されない。

まとめると、WFは単純で解釈が簡単だし、Leakageが発生しにくい。けど、実際のヒストリカルパス(系列の実現値)のみで学習するので、オーバフィットもしやすい。といった感じでしょうか。

2.2 Cross-Validation

機械学習界隈でめちゃめちゃ有名なやつ。Cross-Validation(CV)とは、サンプルデータを分割し、その一部をまず解析して、残る部分でその解析のテストを行い、解析自身の妥当性の検証・確認に当てる手法を指します。下図がわかりやすいです。サンプルデータを赤、青、緑に分割しています。

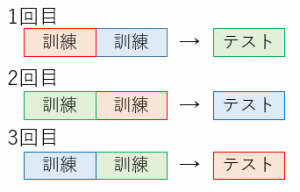
図2 Cross-Validation

CVでバックテストを行う目的は、WFのように過去データに対して正確な性能を導き出すことではなく、多くのアウトオブサンプルのシナリオから将来の性能を推測することにあります。WFが問題として抱えるオーバーフィッティングのしやすさに対処していることになります。

利点
- テストは過去の系列データの結果だけなく、未来(後方)方向をテストデータに持つ結果や逆に過去(前方)データをテストデータに持つものなど、単一のデータセットから未知のアウトサンプルを新たに創造できます。データ系列を逆にして全く異なる結果になる=過学習なので、WFよりマシな方法と言えるかも知れません。
- すべての投資判断は、同じ大きさのデータセットで行われる。これにより、意思決定に使われる情報量が同じという点で、バックテスト結果が比較可能になる。
- すべての観測データがテストデータとして使用される。ウォームアップサブセットがないので、可能な限り長いアウトオブサンプルシミュレーションができる。
欠点
- WFと同様に、単一のバックテストパスがシミュレートされる（ただし、過去のものではない）。観測ごとに生成される予測は1つであり、1つしかない。
- CVには明確な結果解釈ができない(過去の実現値でないので)。バックテスト結果は、投資戦略がどのように過去に実行されたかをシミュレートするのではなく、それが様々なストレスシナリオの下でどのように投資判断を行う可能性があるかをシミュレートする(それ自体が有用な結果であるが)。
- 訓練データとテストデータを必ずしも時系列で繋がっていないため、Leakageが発生する可能性がある。訓練データにテストデータの情報が漏れないように細心の注意を払う必要がある。

2.3 Combinatorial Purged Cross-Validation

Combinatorial Purged Cross-Validation(CPCV)は、WF法とCV法の主な欠点、すなわち、これらのスキームがシングルパスをテストすることに対処した手法になります。
まず、\(T\)個の観測値を入れ替え(シャッフル)なしで\(N\)個のグループに分割します。グループ\(n = 1, ..., N-1\) はサイズ\(T/N\) 、\(N\)個目のグループはサイズ\(T-[T/N](N-1)\)となります。ここで、\([.]\)は整数関数です。\(k\)個のグループをテストデータに回すとすると、可能な訓練/テストデータ分割数は、\(N\)個から\(N-k\)個の訓練データを取得する組み合わせであるので、

\[ \left( \begin{array}{c} N \\ N-k \\ \end{array} \right) = \frac{\prod_{i=0}^{k-1}(N-i)}{k!} \]

となります。各組み合わせには\(k\)個のテスト用グループが含まれるので、テスト用グループの総数は\(k\prod_{i=0}^{k-1}(N-i)/k!\)です。これらのテスト用グループはすべての\(N\)個のグループに一様に分布しています（各グループは同じ数だけ訓練セット、テストセットとして使用されます）。こうすることで、\(N\)個のグループの\(k\)サイズのテストセットから，合計数\(\varphi[N,k]\)のパスをバックテストすることができます。

\[ \varphi[N,k] = \frac{k}{N}\left( \begin{array}{c} N \\ N-k \\ \end{array} \right) = \frac{\prod_{i=1}^{k-1}(N-i)}{(k-1)!} \]

例を考えた方がわかりやすいと思います。今、\(N=6, k=2\)としましょう。ここから、可能な訓練/テストデータ分割数は15個となり、15系列のデータを使用することができます。下図では、それぞれの系列が\(S1,...,S15\)と表されています。

図3 CPCV概念図

上図では、縦軸に分割された6つのグループ、横軸にこれらのグループから4つの訓練データ(と2つのテストデータ)をそれぞれ取得して作成したバックテスト用の全15系列が記載されています。また、各マスに記入されているバツ×はその系列\(Si(i=1,...,15)\)においてそのグループ\(Gi(i=1,...,6)\)がテストデータであることを意味しています(空欄は訓練データを意味)。各グループは\(\varphi[6,2]=5\)回テストデータとして使用されます。よって、このスキームでは5つのバックテストパスを計算することができます。

全てのグループは5回テストデータとして使用され、その1つ1つをそれぞれのバックテストパスに割り当てます。下図では、先ほど×が入力されていたマスに数字が入力されています。それぞれの番号はそれぞれのグループが何番目のバックテストパスに割り当てられたかを示しており、例えば、パス1では15系列のグループ1\(G1\)のうち\((G1,S1)\)が使用され、\((G2,S2),(G3,S2),(G4,S3),(G5,S4),(G6,S5)\)と続いています。

図4 バックテストパスの複数生成

パス2も同様に\((G1,S2),(G2,S6),(G3,S6),(G4,S7),(G5,S8),(G6,S9)\)といった形です。パス3,4,5もこのような形で生成することが可能です(ちなみにこれらの選び方はランダムで良いようです)。
この例では、5つのパスしか生成していませんがサンプルパスが十分長ければCPCVでは何千ものパスを生成することができます。パスの数\(\varphi[N,k]\)は\(N\rightarrow T,k\rightarrow N/2\)になるにつれて長くなります。
CPCVの主な利点は、単一の（オーバーフィットしそうな）シャープレシオの推定値とは対照的に、シャープレシオの分布を導出できることです。WFはもちろん、CVでも複数のバックテストパスは生成することができませんでした。肝は\(k\)を2以上にすることです。\(k=1\)だとCV=CPCVです。

3. バックテストのシミュレーション

2節で見た手法のバックテストシミュレーションをしてみましょう。

まず、最小分散ポートフォリオ(空売制約有)を関数として定義しておきます。こちらは以前の記事で使用した物を流用しています。

同じ関数をそれぞれのバックテスト資料に適用して、比較してみようという算段です。

3.1 Walk Forward シミュレーション

では、まずwalk Forward シミュレーションです。

3.2 Cross Validation

WF <- function(x,k,p){
#------------------------------
# Description 
#  x - data
#  k - sample size of each train set(optimization window)
#  p - sample size of each test set(test window)
#------------------------------

  Time <- seq(1,NROW(x),k+p)
  Time <- Time[Time<=(NROW(x)-k-p)]
  doit <- function(i){
    data <- list(test=x[(i+k+1):(i+k+p),],train=x[i:(i+p-1),])
    return(data)
  }
  res <- lapply(Time, function(i) try(doit(i)))
  return(res)  
}

res <- WF(hist.returns,30,30)
result <- purrr::map(res,function(x){backtest(x,FUN="nlgmv")})

3.3 Combinatorial Purged Cross-Validation

CPCV <- function(x,G,k){
#------------------------------
# Description 
#  x - data
#  G - number of Groups
#  k - number of test Groups on each set
#------------------------------
  
  Time <- round(rep(NROW(x)%/%G,length=G))
  Time[G] <- Time[G] + NROW(x)%%G
  x$index <- rep(c(1:G), times=Time)
  S <- t(combn(G,k))
  doit <- function(i){
    data <- list(test=x[x$index %in% S[i,],-NCOL(x)],train=x[!(x$index %in% S[i,]),-NCOL(data)])
    return(data)
  }
  res <- lapply(1:NROW(S), function(i) try(doit(i)))
  return(res)
}

res <- CPCV(hist.returns,6,2)
result <- purrr::map(res,function(x){backtest(x,FUN="nlgmv")})