【仕事関連】イールドカーブのモデル化について

Nelson-Siegelモデル

NelsonとSiegelが1987にJournal of Businessにパブリッシュした論文です。http://www.jstor.org/stable/2352957

このモデルの特徴は少ないパラメータでイールドカーブの一般的な特徴を記述できるところです。このモデルでは、満期\(m\) ヵ月の無リスクフォワードレート\(f(m)\)を

\[ \begin{eqnarray} f(m)=L+Se−m\lambda+Cm\lambda e−m\lambda \tag{1} \end{eqnarray} \]

と表しています。ここで、\(L\)、\(S\)、\(C\)、\(\lambda\)はパラメータであり、それぞれイールドの水準、傾き、曲率、スケールを決定します。\(y(m)\)を残存\(m\)ヵ月の無リスク割引債のスポットレートだとすると、\(y(m)\)は以下のようなフォワードレート\(f(m)\)の平均金利として表せます。

$$ \[\begin{eqnarray} y(m)&=&\frac{1}{m}\int^m_0f(x)dx \\ &=&\frac{1}{m}\int^m_0(L+Se^{−x\lambda}+Cx\lambda e^{−x\lambda})dx \\ &=&\frac{1}{m}(\int^m_0Ldx+\int^m_0Se^{−x\lambda}dx+\int^m_0Cxλe^{−x\lambda}dx) \tag{2} \end{eqnarray}\] $$

各積分はそれぞれ以下のように計算できます。

$$ \[\begin{eqnarray} \int^m_0Ldx&=&Lm \\ \int^m_0Se^{−x\lambda}dx&=&S[\frac{−e^{−x\lambda}}{\lambda}]^m_0=S(\frac{1}{\lambda}−\frac{e^{−m\lambda}}{\lambda}) \\ \int^m_0 Cx\lambda e^{−x\lambda}dx&=&C\int^m_0(x\lambda e^{−x\lambda}−e^{−x\lambda}+e^{−x\lambda})dx=C[−\frac{e^{−x\lambda}}{\lambda}−xe^{−x\lambda}]^m_0=C(\frac{1}{\lambda}−\frac{e^{−m\lambda}}{\lambda}−me^{−m\lambda}) \end{eqnarray}\] $$

よって、(2)は、

\[ y(m)=\frac{1}{m}(Lm+S(\frac{1−e^{−m\lambda}}{\lambda})+C(\frac{1−e^{−m\lambda}}{\lambda}−me^{−m\lambda}))\tag{3} \]

と表すことができます。先ほど少しパラメータの意味についてご説明しましたが、この形を見ればよりその意味が分かるのではないかと思います。(3)の第一項は定数項なので、全ての残存期間に対して共通の金利水準を表しています（つまり、金利シフトに関わるパラメータ）。第二項は残存期間に対して以下のように単調減少関数となっており、S はイールドカーブの勾配を表していることがわかります。つまり、おおざっぱに言えば、S>0の時は逆イールド、逆の時は順イールドを表現することができるということです。

library(tidyverse)
f1 <- function(m,lambda){
  ((1-exp(-m*lambda))/(m*lambda))
}
plot(1:20,f1(1:20,0.25),type="l",xlab = "Maturity",ylab = "Yield")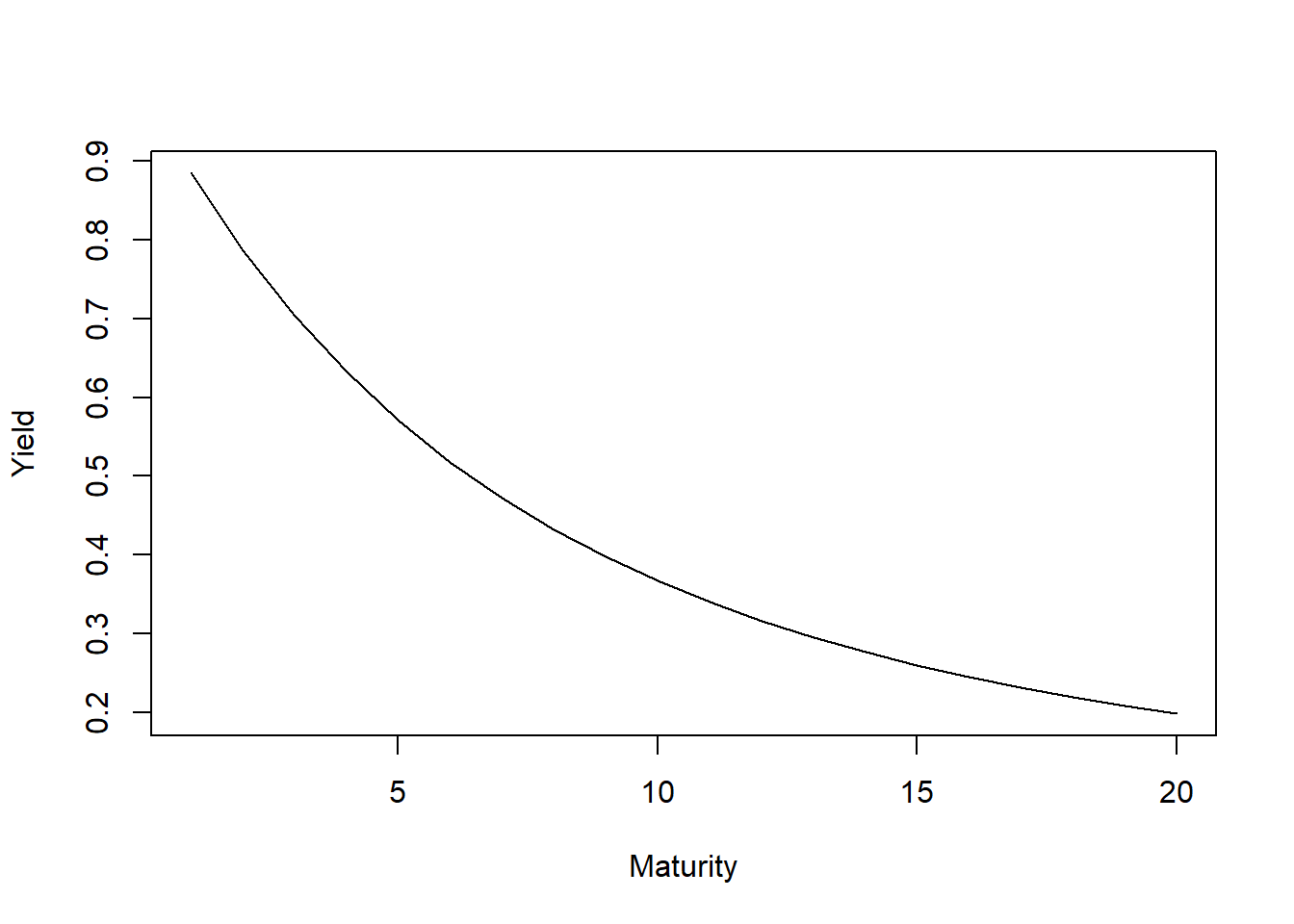

次に、第三項ですがこちらは残存期間に対して上に凸の関数であり、Cは曲率を表していることがわかります。

f2 <- function(m,lambda){
  ((1-exp(-m*lambda))/(m*lambda)-exp(-m*lambda))
}
plot(1:20,f2(1:20,0.25),type="l",xlab = "Maturity",ylab = "Yield")

これらの項を組み合わせると、以下のように見慣れた順イールドカーブを表現することができ、また先述したようにパラメータの値によっては逆イールドも表現でき、また勾配と曲率の組合せによりフラットニングやスティープニングも表現できます。*1

plot(1:20,1.8-1.65*f1(1:20,-0.25)-3*f2(1:20,-0.25),type = "l",xlab = "Maturity",ylab = "Yield")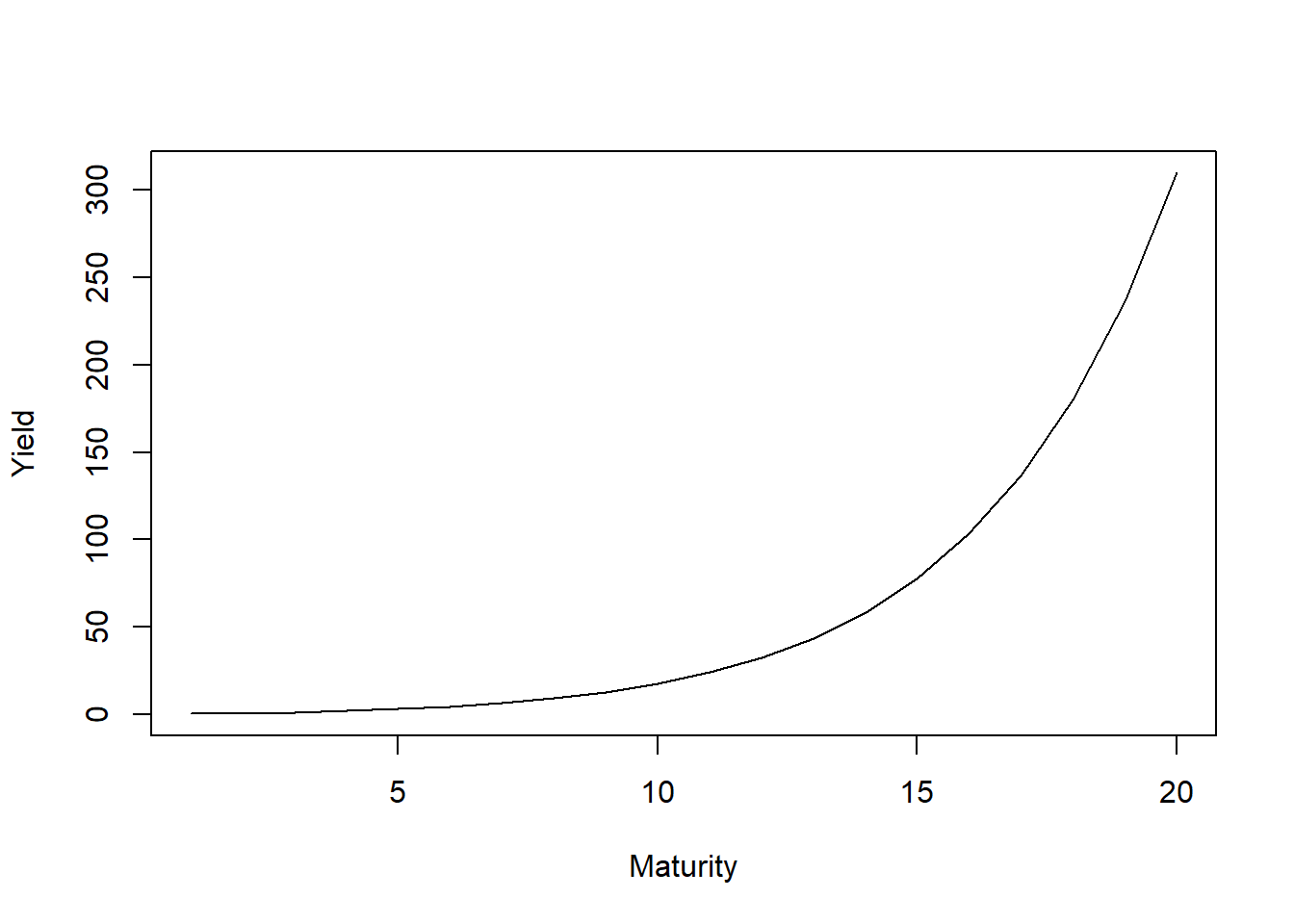

あとは(3)を実際のゼロクーポンを当ててフィッティングすれば良いことになります。ここで、\(L\)、\(S\)、\(C\)に関しては線形なので通常のOLSで推計すればよいことになりますが、\(\lambda\)は非線形関数となっており、optimizerによる収束計算が必要になります。

Rによる推定の実装

推定を行うにあたって必要なものはゼロクーポンイールドですが、今回は財務省のデータ（国債金利情報:財務省）で代用したいと思います。プロットするとこんな感じ（2000年4月~直近）。

library(dplyr)
library(tidyr)
library(ggplot2)
library(scales)
library(xts)
library(plotly)

source.jgb <- "http://www.mof.go.jp/jgbs/reference/interest_rate/data/jgbcm_all.csv"
jgb_all <- read.csv(source.jgb,skip=1)
colnames(jgb_all) <- c("Date","1","2","3","4","5","6","7","8","9","10",
                       "15","20","25","30","40")
jgb_all$Date <- as.character(jgb_all$Date)

# a function to transform Japanese calendar to Western calendar 
ToChristianEra <- function(x)
{
  era  <- substr(x, 1, 1)
  year <- as.numeric(substr(x, 2, nchar(x)))
  if(era == "H"){
    year <- year + 1988
  }else if(era == "S"){
    year <- year + 1925
  } else if(era == "R"){
    year <- year + 2019
  }
  as.character(year)
}

# calendar transformation (Japanese to Western)
jgb.day <- strsplit(jgb_all[,1],"\\.")
warn.old <- getOption("warn")
options(warn = -1)
jgb.day <- lapply(jgb.day, function(x)c(ToChristianEra(x[1]), x[2:length(x)]))
jgb_all[, 1] <- as.Date(sapply(jgb.day, function(x)Reduce(function(y,z)paste(y,z, sep="-"),x)))
jgb_all[, -1] <- apply(jgb_all[, -1], 2, as.numeric)
options(warn = warn.old)
rm(jgb.day)

# create a xts object
jgb.xts <- as.xts(read.zoo(jgb_all))

# 3D plot
jgb.xts["2000::"] %>%
  data.matrix() %>% 
  t() %>%
  plot_ly(
    x=as.Date(index(jgb.xts["2000::"])),
    y=c(1,2,3,4,5,6,7,8,9,10,15,20,25,30,40),
    z=.,
    type="surface"
  ) %>%
  plotly::layout(
    scene=list(
      xaxis=list(title="date"),
      yaxis=list(title="term"),
      zaxis=list(title="yield")
    )
  )

金利は低下傾向であり、また2010年の前と後では短期ゾーンの形状が変わっていることもわかると思います。つまり、これは先述したパラメータが一定ではないことを意味しており、各時期のイールドカーブにフィッティングするためには時変パラメータの推定が必要であることを示唆しています。当たり前といえば当たり前ですが、しかしパラメータが推定期間に対して安定性がないのではモデルとしてはいまいちなのではと思ってしまいます。

では、固定パラメータの推計に移ります。Nelson and Siegel(1987)では\(\lambda\)の値を先に決め、その後でほかのパラメータをOLS推計することを繰り返し、決定係数が最大になる点を推定値としています。とりあえず、こちらもこの推計方法に従いたいと思います。まず推計用のデータセットを作成します。

# create dataset
dataset <- jgb_all %>%
  tidyr::gather(key = "maturity", value = "irate",
                "1","2","3","4","5","6","7","8","9","10","15","20","25","30","40")
head(dataset)

##         Date maturity  irate
## 1 1974-09-24        1 10.327
## 2 1974-09-25        1 10.333
## 3 1974-09-26        1 10.340
## 4 1974-09-27        1 10.347
## 5 1974-09-28        1 10.354
## 6 1974-09-30        1 10.368

次に、決定係数を最大化するために目的関数を定義します。この目的関数は\(\lambda\)を入力値とし、その値に応じて(5)式の第二項、第三項を計算します。そして、それらを説明変数、財務省から取得したイールドデータを非説明変数とする重回帰を実施し、その決定係数を返します。

# define objective function
obj.func <- function(lambda,dataset,time_end,time_start){
  f1 <- function(m,lambda){
    ((1-exp(-m*lambda))/(m*lambda))
    }
  f2 <- function(m,lambda){
    ((1-exp(-m*lambda))/(m*lambda)-exp(-m*lambda))
    }
  dataset <- dataset %>%
    mutate(f1 = f1(as.numeric(dataset$maturity)*12,lambda), f2 = f2(as.numeric(dataset$maturity)*12,lambda))
  results <- lm(0.01*irate ~ f1 + f2,data = dataset,subset = (Date>time_start & time_end>Date))
  return(summary(results)$r.squared)
}

Rのoptimaze関数で最適化を行います。サンプル自体は1974年からありますが、国債流通市場が機能し始めたのは1980年代後半の金利自由化以降であり、また残存期間10年超の国債が安定的に取引されていたのは1990年以降であるので、1992年以降のサンプルを使用して推計を行います（それまではNAがたくさん）。\(\lambda\)はNelson and Siegel(1987)と同じく1/200~1/10の間で探索を行います。

test <- optimize(obj.func,interval = c(1/10,1/200),dataset=dataset,time_start="1992-01-01",time_end="2019-07-01",maximum = TRUE)
test

## $maximum
## [1] 0.06429411
## 
## $objective
## [1] 0.140107

決定係数を最大にする\(\lambda\)は0.0642941であり、その時の決定係数は0.140107という結果になりました。いや、決定係数低すぎるなぁ。やはり、先ほどお示ししたように2010年（もしかするとリーマン）の前後でイールドカーブの形状が大きく変わっており、また全ての残存期間で金利が低下傾向ということが原因であると思います。やはり、固定パラメータでは全サンプルに対する当てはまりが悪い。安直な手ですが、サンプル期間を2010年で分断し、推計を二回行ってみます。もちろん、決定係数にこだわりすぎることは危険ではあるのですが、これではモデルを使用している意味がないほど当てはまりが悪いので。

# 1992-01-01~2009-12-31で推計
optimize(obj.func,interval = c(1/10,1/200),dataset=dataset,time_end="2010-01-01",time_start="1992-01-01",maximum = TRUE)

## $maximum
## [1] 0.06885455
## 
## $objective
## [1] 0.1891524

# 2010-01-01~2019-07-01で推計
optimize(obj.func,interval = c(1/10,1/200),dataset=dataset,time_end="2019-07-01",time_start="2010-01-01",maximum = TRUE)

## $maximum
## [1] 0.02284422
## 
## $objective
## [1] 0.6290687

どうやら2010年以降のサンプルでは当てはまり良いようです。この\(\lambda\)の値を用いて、OLS推計を行います。

lambda = 0.02290492
dataset <- dataset %>%
  mutate(f1 = f1(as.numeric(dataset$maturity)*12,lambda), f2 = f2(as.numeric(dataset$maturity)*12,lambda))
head(dataset)

##         Date maturity  irate       f1        f2
## 1 1974-09-24        1 10.327 0.874342 0.1146628
## 2 1974-09-25        1 10.333 0.874342 0.1146628
## 3 1974-09-26        1 10.340 0.874342 0.1146628
## 4 1974-09-27        1 10.347 0.874342 0.1146628
## 5 1974-09-28        1 10.354 0.874342 0.1146628
## 6 1974-09-30        1 10.368 0.874342 0.1146628

results <- lm(0.01*irate ~ f1 + f2,data = dataset,subset = (Date>"2010-01-01" & "2019-07-01">Date))

summary(results)

## 
## Call:
## lm(formula = 0.01 * irate ~ f1 + f2, data = dataset, subset = (Date > 
##     "2010-01-01" & "2019-07-01" > Date))
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -0.0149407 -0.0027083  0.0004238  0.0026368  0.0104803 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  2.006e-02  7.495e-05   267.7   <2e-16 ***
## f1          -1.881e-02  9.863e-05  -190.7   <2e-16 ***
## f2          -3.012e-02  3.181e-04   -94.7   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.004161 on 34872 degrees of freedom
## Multiple R-squared:  0.6291, Adjusted R-squared:  0.629 
## F-statistic: 2.957e+04 on 2 and 34872 DF,  p-value: < 2.2e-16

推計したイールドカーブをプロットしたのが以下です。

maturity <- 1:600
plot(maturity,results$coefficients[1]+results$coefficients[2]*f1(maturity,lambda)+results$coefficients[3]*f2(maturity,lambda),type = "l",xlab = "Maturity",ylab = "Yield")

まあこんな感じですかね。とりあえず、イールドカーブの推計はできました。

パフォーマンス要因分解とイールドカーブモデル

そもそもイールドカーブモデルはパフォーマンス要因分解のどこで使用するのでしょうか？以下のような参考文献を見つけました。p22のAppendix2にその説明があります。

http://summit.sfu.ca/system/files/iritems1/762/FRM%202010%20Melnikov,%20A.%20Simic,%20S..pdf

以下引用 FIXED INCOME ATTRIBUTION: ANALYZING SOURCES OF RETURN Appendix2: DMT (at t-1) is a treasury rate on a 2.14 year treasury bill at the beginning of the attribution period. DMT (at t) is a treasury rate on a 2.14 year treasury bill at the end of the attribution period. It is unlikely that we are going to find 2.14 year treasury bill trading in the market at any given point in time. As such, we will be required to interpolate it’s yield from a standard treasury yield curve. There are several choices available for interpolation, with the simplest one being linear interpolation. Models that are more complex may apply quadratic, cubic interpolation, or Nelson-Siegel (1987) approach. As long as interpolation approach is consistent for both benchmark and portfolio, the bias is kept to minimum.

トータルリターンをシフト効果とツイスト効果に分解する際に、Duration-matched Tresury rateを計算する必要があるらしく、その際にイールドカーブモデルが必要になるとのことです。保有している債券のデュレーションはパフォーマンス計測期間にきっちり整数値をとるとは限りませんが、市場には例えば2.14のデュレーションを持つ債券は常にありそうにはないので当然です。ただ、Nelson Siegelモデルを使用するほかにも、線形補間や2次、3次補間を行うこともあるようです。こうして考えてみると、このモデルをパフォーマンス要因分解が目的で使用するのであれば、推計時点でパラメータの安定性がないことにさほど問題はないように思われます。時系列分析に使用するのが問題のような気がしてきました（いくつかペーパーがありますが）。基本的に補間のために作られたモデルと理解した方が良さそうです。Appendix3では各要因分解の計算方法が掲載されているので、それを見て今回の記事は終わりにしたいと思います。トータルリターンは以下のように、①Income、②Shift、③Twist、④Spread、⑤Selectionに分解することができます。

$$

Income=\

Shift=−Duration×ΔKRD \

Twist=−Duration×(ΔDMT−ΔKRD) \

Spread=−Duration×() \

Selection=TotalReturn−Income−Shift−Twist−Spread

$$