おはこんばんにちは。前回の記事でGoogl Earth Engineから衛星画像データを取得しました。ですが、ipygeeという素晴らしいツールがあり、より簡単に時系列データを取得できることがわかりました。今回はipygeeでデータを取得し、それを用いて景況感のナウキャスティングをやってみます。
import pandas as pd
import matplotlib.pyplot as plt
import os
import datetime
import ipygee
import ee
from sklearn.preprocessing import MinMaxScaler
ee.Initialize()
os.environ['QT_QPA_PLATFORM_PLUGIN_PATH'] = 'C:/Users/aashi/Anaconda3/envs/earthengine/Library/plugins/platforms'
plt.style.use('ggplot')
plt.xkcd()## <matplotlib.rc_context object at 0x000000001EC99FD0>まず、FeatureCollectionとImageCollectionメソッドを使用して、日本の地理データと夜間光の衛星画像データを取得します。
start = datetime.datetime(2014,1,1)
end = datetime.datetime(2019,1,1)
japan = ee.FeatureCollection('ft:1tdSwUL7MVpOauSgRzqVTOwdfy17KDbw-1d9omPw').filter(ee.Filter.eq('Country', 'Japan'))
dataset = ee.ImageCollection('NOAA/VIIRS/DNB/MONTHLY_V1/VCMSLCFG').filter(ee.Filter.date(start,end)).select('avg_rad')あとは、取得したImageCollectionを日本の地理データに形どり、夜間光を集計するipygee.chart.ImageのseriesByRegionメソッドを使用し、pandasデータフレームへ変換します。
chart_ts_region = ipygee.chart.Image.seriesByRegion(**{
'imageCollection': dataset,
'reducer': ee.Reducer.sum(),
'regions': japan,
'scale': 1000
})
nightjp = chart_ts_region.dataframe
nightjp.columns = ['nightlight']
nightjp.index = nightjp.index + pd.tseries.offsets.MonthEnd(1)
nightjp.head()## nightlight
## 2014-01-31 881528.746399
## 2014-02-28 827364.583605
## 2014-03-31 729127.359961
## 2014-04-30 612680.682750
## 2014-05-31 661449.531736ここまでやってしまえば、あとはpandasデータフレームですからpythonでの解析が可能になります。そもそもeeのみでは、javascriptで使用できたui.chartメソッドを使用することができませんでした。よって、時系列データを取得するためにはee上でデータを作り、それをgoogle driveへexportし、pandas.read_csvで読み取るといったまどろっこしい作業をしなければなりませんでした。これなら関数1つで取得できますからかなり便利です。グラフにするとこんな感じです。前回取得したデータと同じようなデータが取得できています。
nightjp.plot()
plt.show()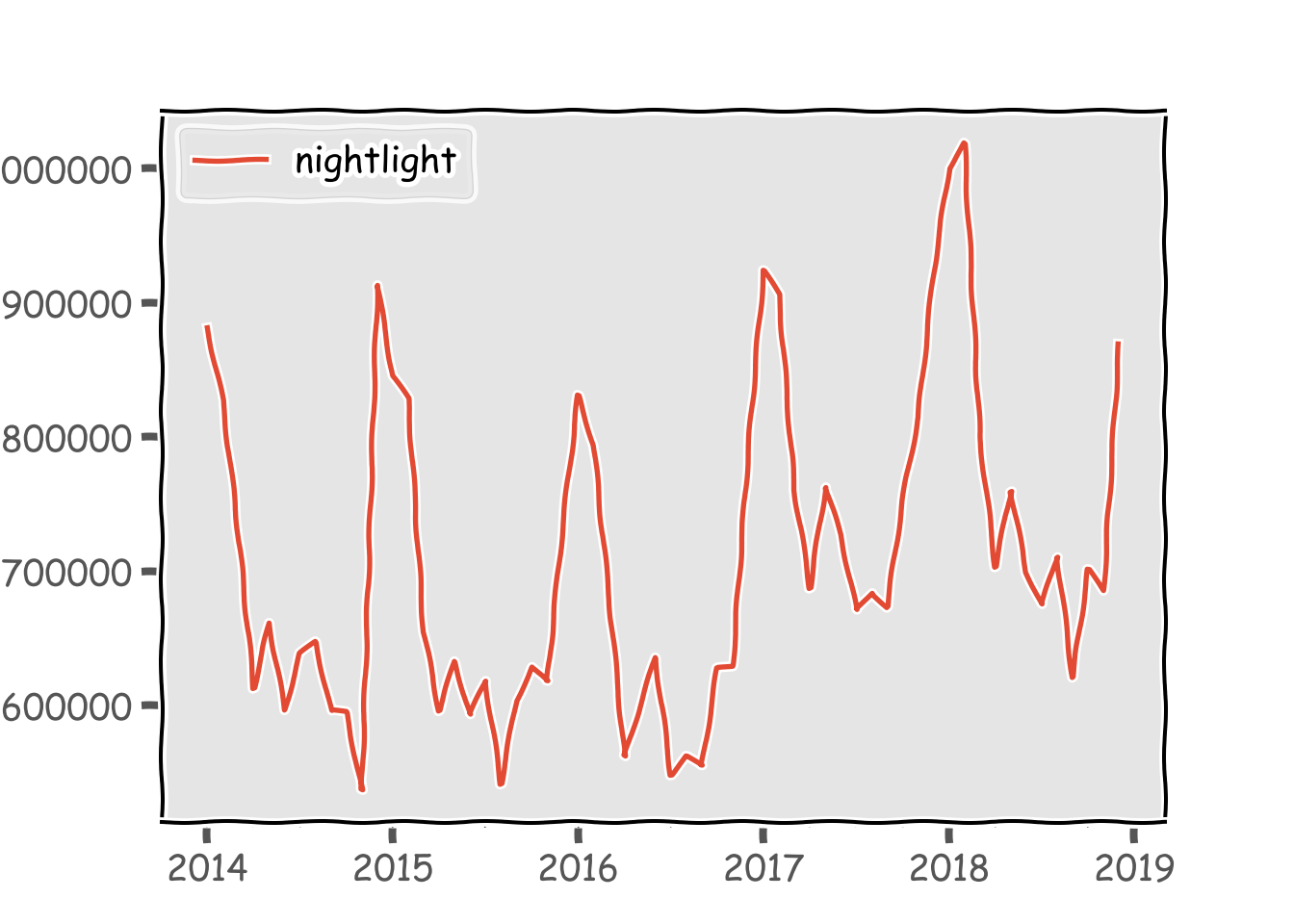
ここからは解析に移りたいのですが、御覧の通りかなり季節性があることがわかります。どうやら冬場に光量が大きくなる傾向になるようです(そもそも日が短いので)。なので、季節調整をかけてみます。RではX-13ARIMA-SEATSをいつも使用していますが、pythonでの使い方がわからないので、statsmodels.apiのseasonal_decomposeを使います。冬場とそれ以外で挙動が異なるのでfreqは12にしてみました。
import statsmodels.api as sm
nightjp_sm = sm.tsa.seasonal_decompose(nightjp['nightlight'],freq=12,model='multiplicative')
nightjp_sm.plot()
plt.show()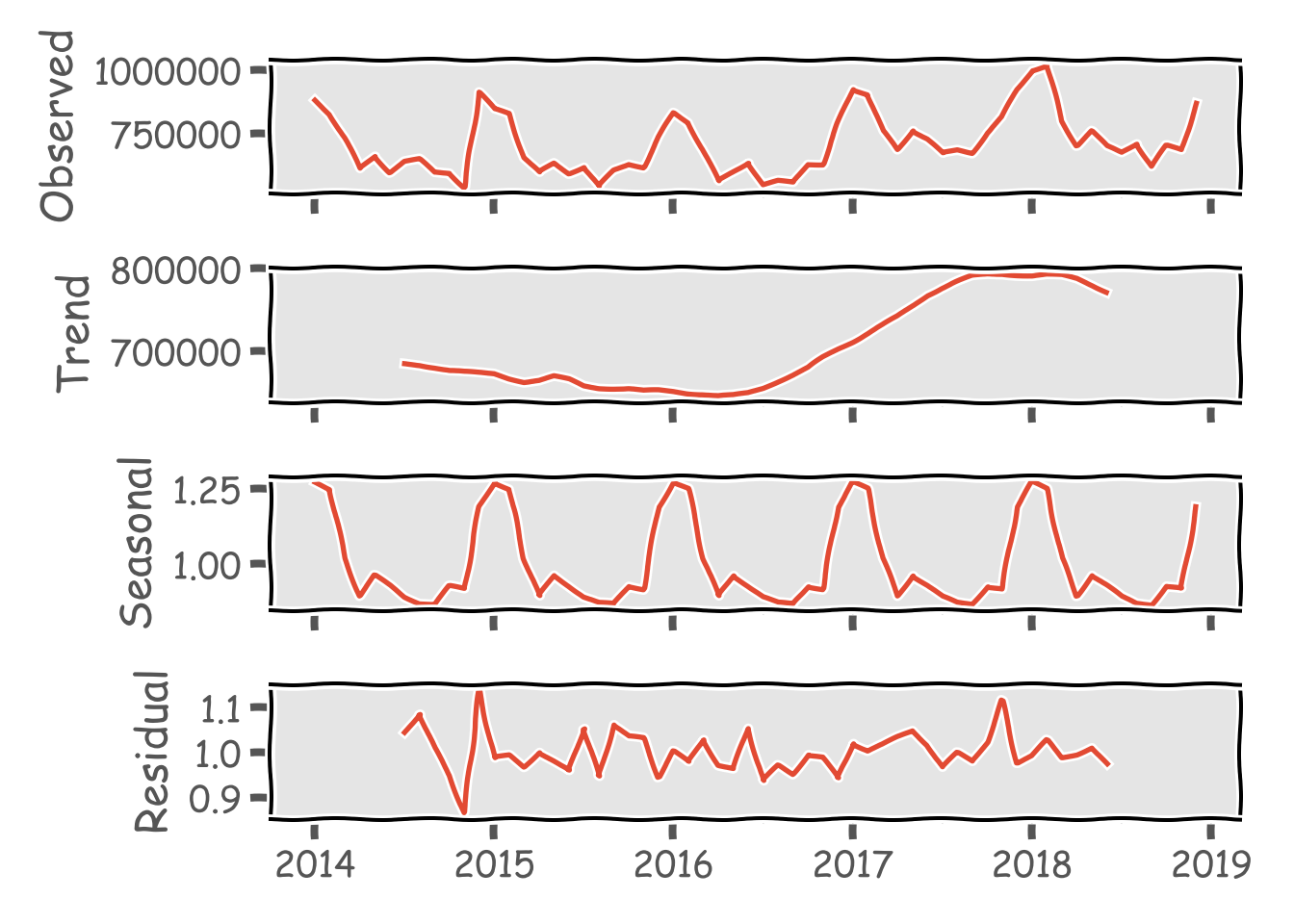
季節性を除いたTrendが2016年半ばくらいから2017年下旬にかけて急激に上昇しています。おそらく、景況感とはあまり相関がなさそうな動きをしていますが、以下の記事を参考にestatからAPIで鉱工業生産指数のデータを落とし、検証してみます。
http://sinhrks.hatenablog.com/entry/2015/12/31/222207
import numpy as np
import japandas as jpd
# import IIP from estat api
dlist = jpd.DataReader("00550300", 'estat', appid=key)
tables = dlist[(dlist['統計表題名及び表番号'].str.contains('総合季節調整済指数【月次】 付加価値額生産')) & (dlist['提供統計名及び提供分類名'].str.contains('鉱工業生産・出荷・在庫指数'))]
data = jpd.DataReader(tables.iloc[0,0], 'estat', appid=key)
df = data[(data['業種別'].str.contains('1000000000 鉱工業')) & ~(data['統計項目A_2015_Match'].str.contains('付加生産ウエイト')) & ~(data['統計項目A_2015_Match'].str.contains('p'))]
df.index = pd.to_datetime(df["統計項目A_2015_Match"], format="%Y%m") + pd.tseries.offsets.MonthEnd(1)
df.head()
# merge with seasonally adjusted nightlight data## value 業種別 統計項目A_2015_Match
## 統計項目A_2015_Match
## 2013-01-31 94.8 1000000000 鉱工業 201301
## 2013-02-28 96.5 1000000000 鉱工業 201302
## 2013-03-31 97.7 1000000000 鉱工業 201303
## 2013-04-30 97.7 1000000000 鉱工業 201304
## 2013-05-31 99.3 1000000000 鉱工業 201305df2 = pd.merge(nightjp_sm.trend.to_frame(),df,how='left',left_index=True,right_index=True)[['nightlight','value']]
df2.head()
# MinMaxScaling## nightlight value
## 2014-01-31 NaN 103.8
## 2014-02-28 NaN 102.7
## 2014-03-31 NaN 104.2
## 2014-04-30 NaN 99.6
## 2014-05-31 NaN 101.9scaler = MinMaxScaler()
df2.loc[:,['nightlight','value']] = scaler.fit(df2).transform(df2)
df2.plot()
plt.show()
予想に反し、かなり良い傾向を掴めていますね。季節調整を少し雑にやっているので、必要な情報もノイズとしてスクリーニングされた感がありますが、季節調整を真面目にやればかなり近い数値が出てくる気もします。ということで、X-13ARIMA-SEATSのpythonでの使い方をググりました。なんとstatsmodelsで動かせるようです。
import statsmodels as sms
# x13
os.environ['X13PATH'] = r"C:\Program Files\WinX13\x13as"
x13results = sms.tsa.x13.x13_arima_analysis(endog = nightjp['nightlight'],prefer_x13=True)
x13results.plot()
# merge with seasonally adjusted nightlight data
df3 = pd.merge(x13results.seasadj.to_frame(),df,left_index=True,right_index=True)[['seasadj','value']]
# MinMaxScaling
scaler = MinMaxScaler()
df3.loc[:,['seasadj','value']] = scaler.fit(df3).transform(df3)
df3.plot()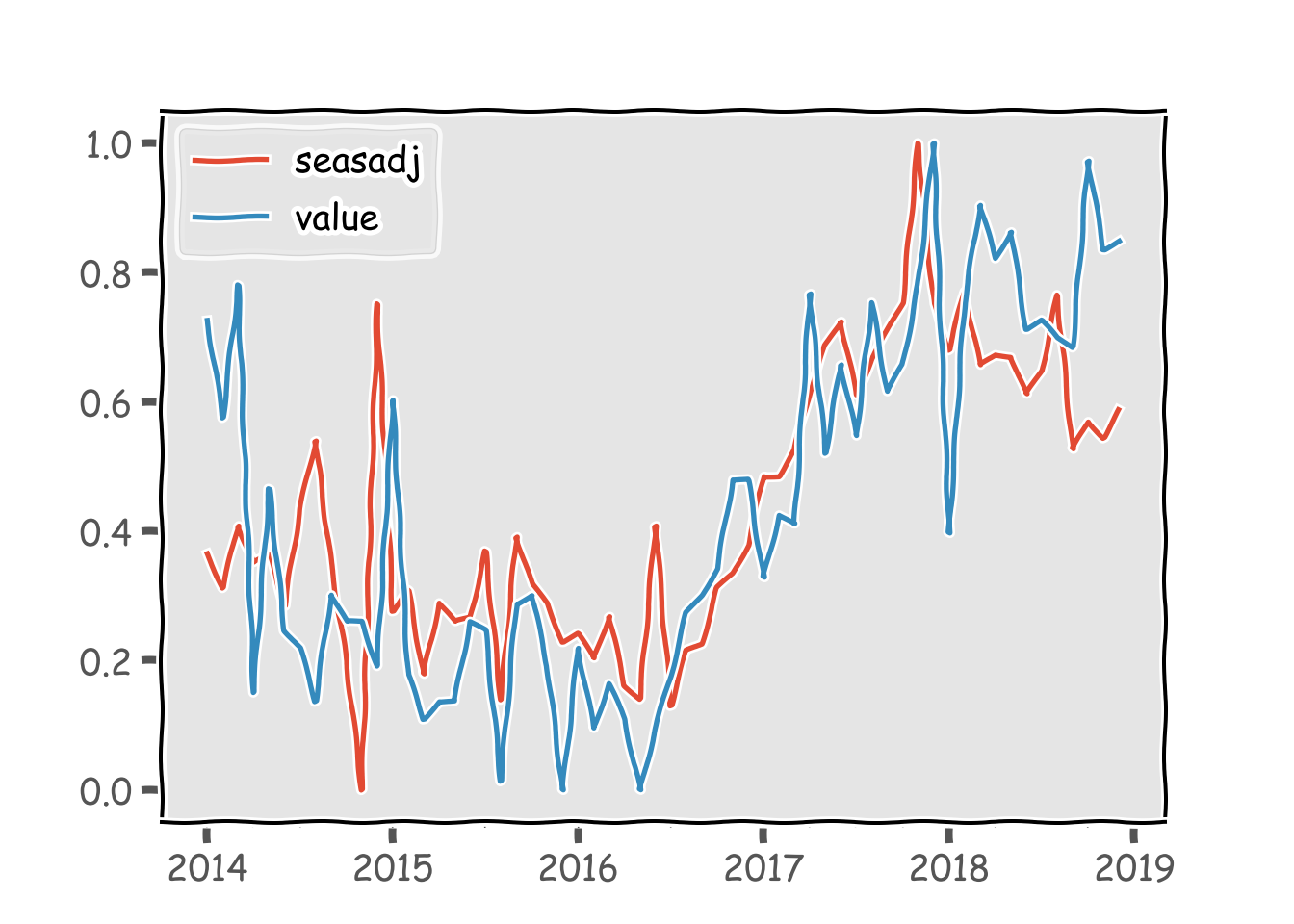
そこそこ説明力高め。これは個人的には大発見です。鉱工業生産指数はGDPとの相関が高く、月次統計でもあります。ただ、生産動向統計から作成されると言うこともあり、データが公表されるタイミングは速報値が出るのが翌月末です。一方、衛星データであれば月初から推計値を計算することが可能です。まさにナウキャスティングですね。欲を言えば、日次でデータが取れれば最高なんですけどね。多分それは有料ならできるんでしょう。。。今はこれで我慢です。(いつか使える日が来るのか?)
単回帰もやってみます。
from sklearn import linear_model
clf = linear_model.LinearRegression(normalize=False)
X = df3.dropna().loc[:, ['seasadj']].as_matrix()## C:/Users/aashi/Anaconda3/envs/earthengine/python.exe:1: FutureWarning: Method .as_matrix will be removed in a future version. Use .values instead.Y = df3.dropna()['value'].as_matrix()
clf.fit(X, Y)## LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None,
## normalize=False)print(clf.coef_,clf.intercept_,clf.score(X, Y))## [0.94721098] 0.01956484094473454 0.5228197194050053plt.scatter(X, Y)
plt.plot(X, clf.predict(X))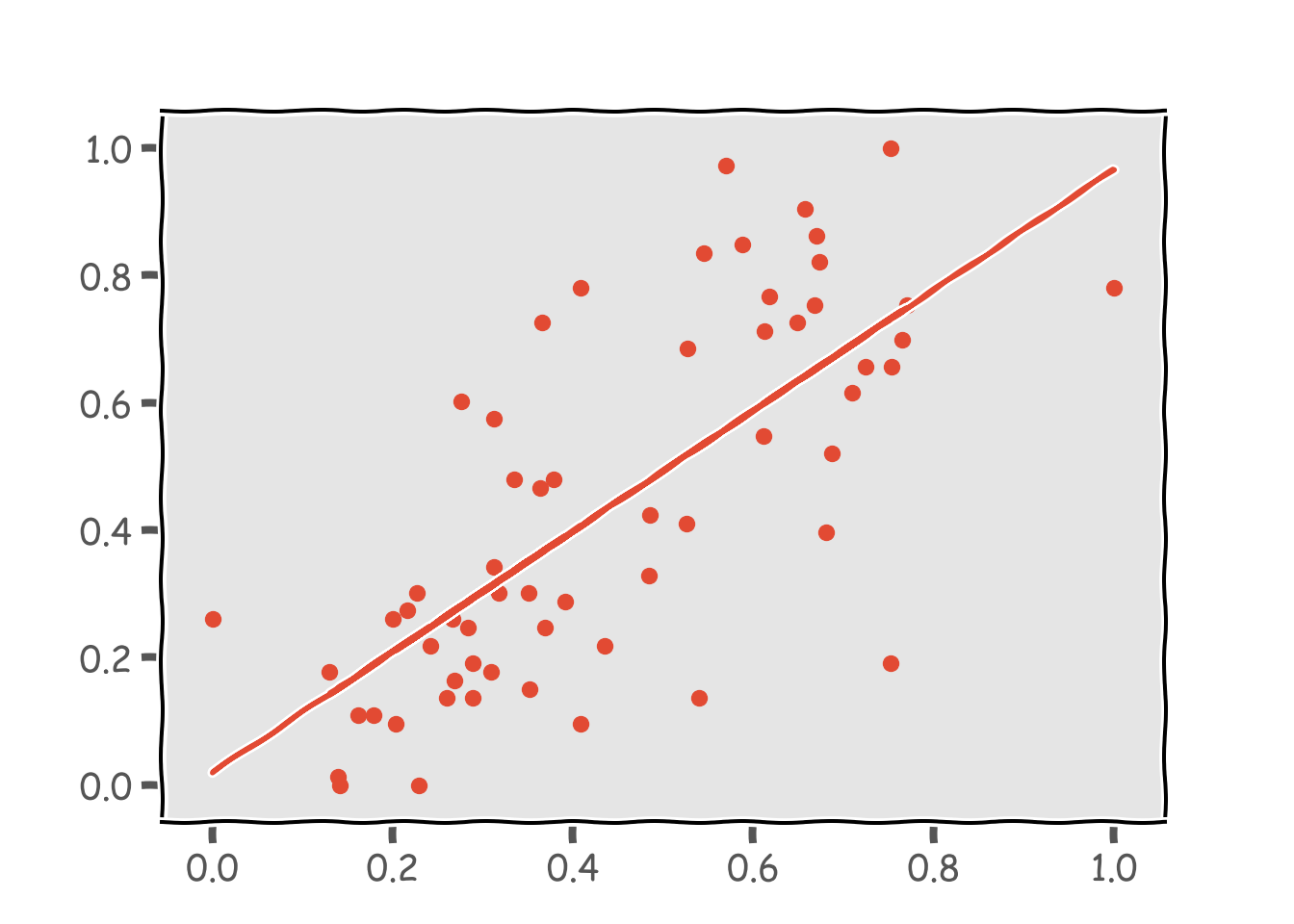
ほぼほぼ比例の関係にありますね。決定係数は0.5でした。散布図を見ると非線形の関係にあるようにも見えるのでガウス回帰でそれも試してみます。
from sklearn.gaussian_process.kernels import RBF,WhiteKernel
from sklearn.gaussian_process import GaussianProcessRegressor as GPR
# kernel is RBF + white
kernel = 1*RBF()+WhiteKernel()
# estimate gp
gp = GPR(kernel,alpha=0)
gp.fit(X,Y)
# plot## GaussianProcessRegressor(alpha=0, copy_X_train=True,
## kernel=1**2 * RBF(length_scale=1) + WhiteKernel(noise_level=1),
## n_restarts_optimizer=0, normalize_y=False,
## optimizer='fmin_l_bfgs_b', random_state=None)X1 = np.linspace(0,1,25000)
plt.plot(X,Y,'. ')
mu,std = gp.predict(X1.reshape(-1, 1),return_std=True)
plt.plot(X1,mu,'g')
plt.fill_between(X1,mu-std,mu+std,alpha=0.2,color='g')
plt.show()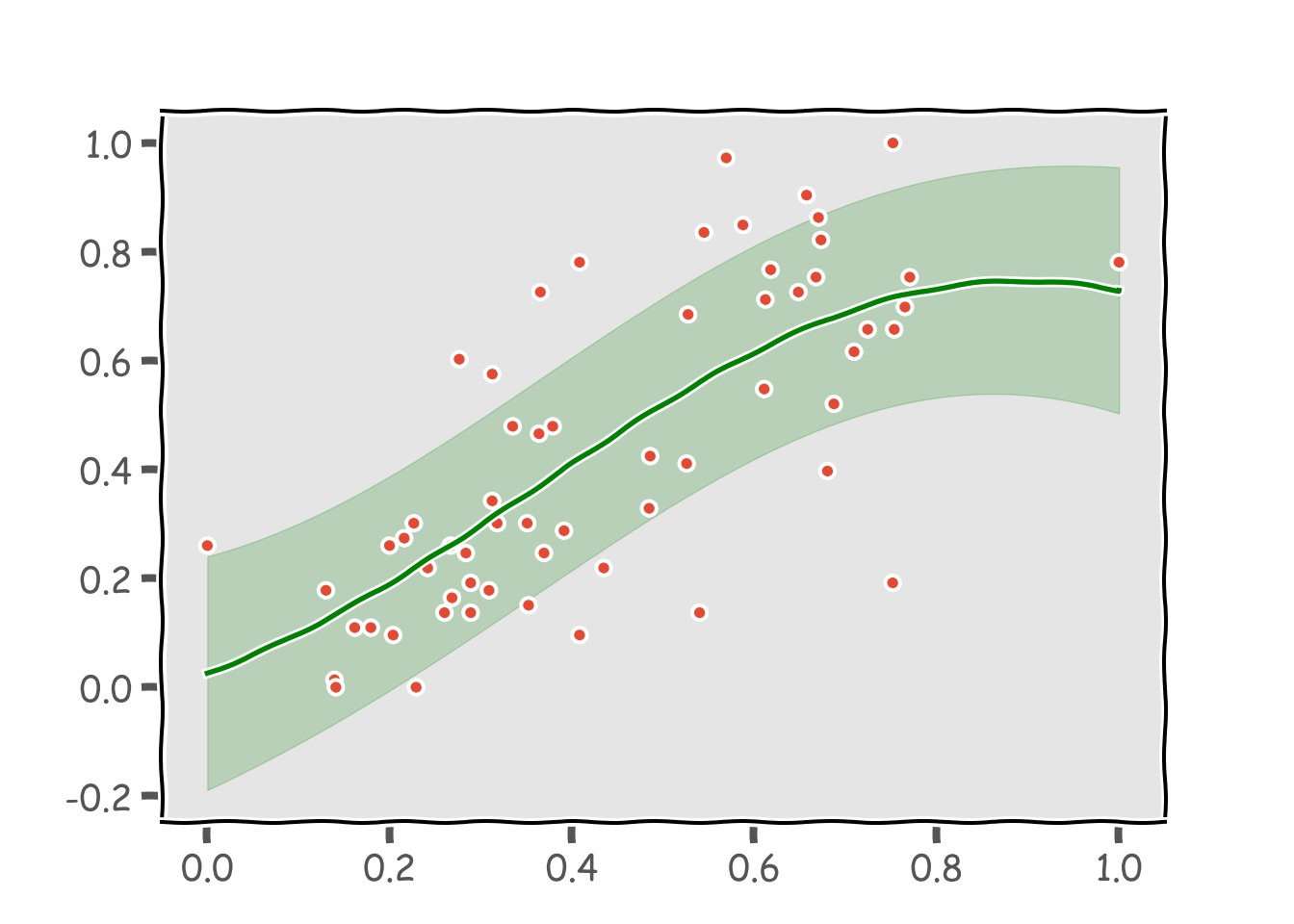
0.6まではほぼ直線ですが、その先で外れ値に引っ張られています。本当は0.7~0.8のところで二次関数のようにぐっと上昇して欲しいのですが。外れ値に引っ張られないよう、正規分布でなくt分布を仮定したt過程回帰で推計します。
実際の推計をする前に、理論的な話をしておきます。そもそもt分布とは正規分布の分散を増減させるパラメータを新たに与え、それがガンマ分布に従うと仮定した分布です。t過程はガウス過程と同様、有限集合\(\textbf{X}\)が入力として与えられた際に、関数値ベクトル\(\textbf{f}_{TP}\)の分布がその多変量t分布に従うような確率分布を言います。t過程は自由度\(v\)、平均関数\(\mu\)、共分散関数を要素に持つ共分散行列\(\textbf{K}\)をパラメータとしています。これを\(\textbf{f}_{TP}\)~\(T(v,\mu(\textbf{x}),\textbf{K}(\textbf{x},\textbf{x}'))\)と表します。\(T(v,\mu(\textbf{x}),\textbf{K}(\textbf{x},\textbf{x}'))\)は先述の通り多変量t分布です。出力である確率変数\(\textbf{y}\)に対して、確率密度関数は以下のように与えられます(つまり多変量t分布の密度関数)。
\[ T(v,\mu,\textbf{K}) = \frac{\Gamma(\frac{v+n}{2})}{((v-2)\pi)^{n/2}\Gamma(\frac{v}{2})}\frac{1}{\sqrt(\det\textbf{K})}(1+\frac{(\textbf{y}-\mu)^T\textbf{K}^{-1}(\textbf{y}-\mu)}{v-2})^{-\frac{(v+n)}2} \]
ここで、\(\Gamma\)はΓ関数です。ここで、\(v\to\infty\)とするとカーネルの部分が、
\[ \lim_{v\to\infty}(1+\frac{(\textbf{y}-\mu)^T\textbf{K}^{-1}(\textbf{y}-\mu)}{v-2})^{-\frac{(v+n)}2}=\exp(\frac{(\textbf{y}-\mu)^T\textbf{K}^{-1}(\textbf{y}-\mu)}{2}) \]
と正規分布に収束するので、先述の通りt分布は正規分布の一般系であることがわかります。次に、今定義したt過程を使った回帰問題について考えます。学習データ\((\textbf{x}_i,y_{i})\)が手元にあるとします。t過程回帰では以下のようなモデルを考えます。
\[ y_{i} = f_{TP}(\textbf{x}_{i}) + \epsilon_{i} \] ここで、\(f_{TP}(\textbf{x}_{i})\)は基底関数による入力ベクトルの特徴量、\(\epsilon_{i}-T(v,0,\sigma^2)\)は観測ノイズを表しています。また、\(\textbf{f}_{TP}=[f_{TP}(\textbf{x}_{1}),...,f_{TP}(\textbf{x}_{n})]^T\)と定義し、t過程に従うとします。\(\textbf{f}_{TP}\)と\(\epsilon_{i}\)の分布がわかっていますから、\(\textbf{x}\)が既知となった後の\(\textbf{y}\)の分布を計算することができます。これはガウス過程の時と同じで、2つの独立なt分布のたたみ込みになるので、\(\textbf{y}-T(v,\mu(\textbf{x}),\textbf{K}(\textbf{x},\textbf{x}')+\sigma\textbf{I})\)となります。この分布を推定するには\(\mu,\textbf{K},\sigma\)を推定する必要があります。まあ、だいたい\(\mu=0,\sigma=1/100\)みたいに決め打ちしてしまうことが多い気がします。重要なのは\(\textbf{K}\)です。これもガウス過程と同じでカーネル関数を用いることで計算の効率化を図ります。どのカーネル関数を用いるかで推定すべきパラメータの数は変わってきますからここでは大まかな推定方法について説明したいと思います。
パラメータの推定方法は最尤法です。カーネル関数を\(K(\textbf{x},\textbf{x}',\beta)\)と定義し、\(\beta\)をパラメータとします。尤度関数は以下で与えられます。
\[ L(v,\mu,\textbf{K}(\textbf{x},\textbf{x}',\beta),\textbf{y}) = \frac{\Gamma(\frac{v+n}{2})}{((v-2)\pi)^{n/2}\Gamma(\frac{v}{2})}\frac{1}{\sqrt(\det\textbf{K}(\textbf{x},\textbf{x}',\beta))}(1+\frac{(\textbf{y}-\mu)^T\textbf{K}(\textbf{x},\textbf{x}',\beta)^{-1}(\textbf{y}-\mu)}{v-2})^{-\frac{(v+n)}2} \]
これを最大化するような\(\beta\)をPCのパワーを使って探索的に求め、最尤推定値とするのです。ここらへんもガウス過程と同じです。これで回帰推定は完了です。とりあえずここまでをpythonで実行しましょう。
import GPy
kernel = GPy.kern.MLP(1, ARD=True)
tpmodel = GPy.models.TPRegression(X.reshape(-1,1),Y.reshape(-1,1),kernel=kernel,normalizer=True)
tpmodel.optimize()## <paramz.optimization.optimization.opt_lbfgsb object at 0x00000000354B4E10>tpmodel.plot()## {'dataplot': [<matplotlib.collections.PathCollection object at 0x00000000386A96A0>], 'gpconfidence': [<matplotlib.collections.PolyCollection object at 0x00000000386A9B38>], 'gpmean': [[<matplotlib.lines.Line2D object at 0x00000000386A94E0>]]}plt.show()
あまり、GPと変化ありませんね。ハイパーパラメータを点推定していますが、MCMCを用いてサンプリングする方法も試してみましょう。
tpmodel.randomize()
hmc = GPy.inference.mcmc.HMC(tpmodel)
sample = hmc.sample(num_samples=10000,hmc_iters=200)## C:\Users\aashi\Anaconda3\envs\earthengine\lib\site-packages\paramz\transformations.py:111: RuntimeWarning:overflow encountered in expm1import seaborn as sns
param_name = tpmodel.parameter_names()
fig, ax = plt.subplots(figsize=(10,4))
ax.set_yscale('log')
sns.boxenplot(data=sample, ax=ax)
ax.set_xticklabels(param_name)## [Text(0, 0, 'mlp.variance'), Text(0, 0, 'mlp.weight_variance'), Text(0, 0, 'mlp.bias_variance'), Text(0, 0, 'deg_free')]fig.tight_layout()
plt.show()
for ii in range(len(param_name)):
tpmodel[param_name[ii]] = np.mean(sample, axis=0)[ii]
tpmodel.plot()
plt.tight_layout()## {'dataplot': [<matplotlib.collections.PathCollection object at 0x0000000005077710>], 'gpconfidence': [<matplotlib.collections.PolyCollection object at 0x0000000005077B70>], 'gpmean': [[<matplotlib.lines.Line2D object at 0x00000000050775F8>]]}
## {'dataplot': [<matplotlib.collections.PathCollection object at 0x000000000521EFD0>], 'gpconfidence': [<matplotlib.collections.PolyCollection object at 0x0000000005224470>], 'gpmean': [[<matplotlib.lines.Line2D object at 0x000000000521EEB8>]]}
## {'dataplot': [<matplotlib.collections.PathCollection object at 0x0000000004619550>], 'gpconfidence': [<matplotlib.collections.PolyCollection object at 0x0000000004619BA8>], 'gpmean': [[<matplotlib.lines.Line2D object at 0x0000000004874470>]]}
## {'dataplot': [<matplotlib.collections.PathCollection object at 0x00000000045F9080>], 'gpconfidence': [<matplotlib.collections.PolyCollection object at 0x00000000045F9470>], 'gpmean': [[<matplotlib.lines.Line2D object at 0x00000000047F1D30>]]}plt.show()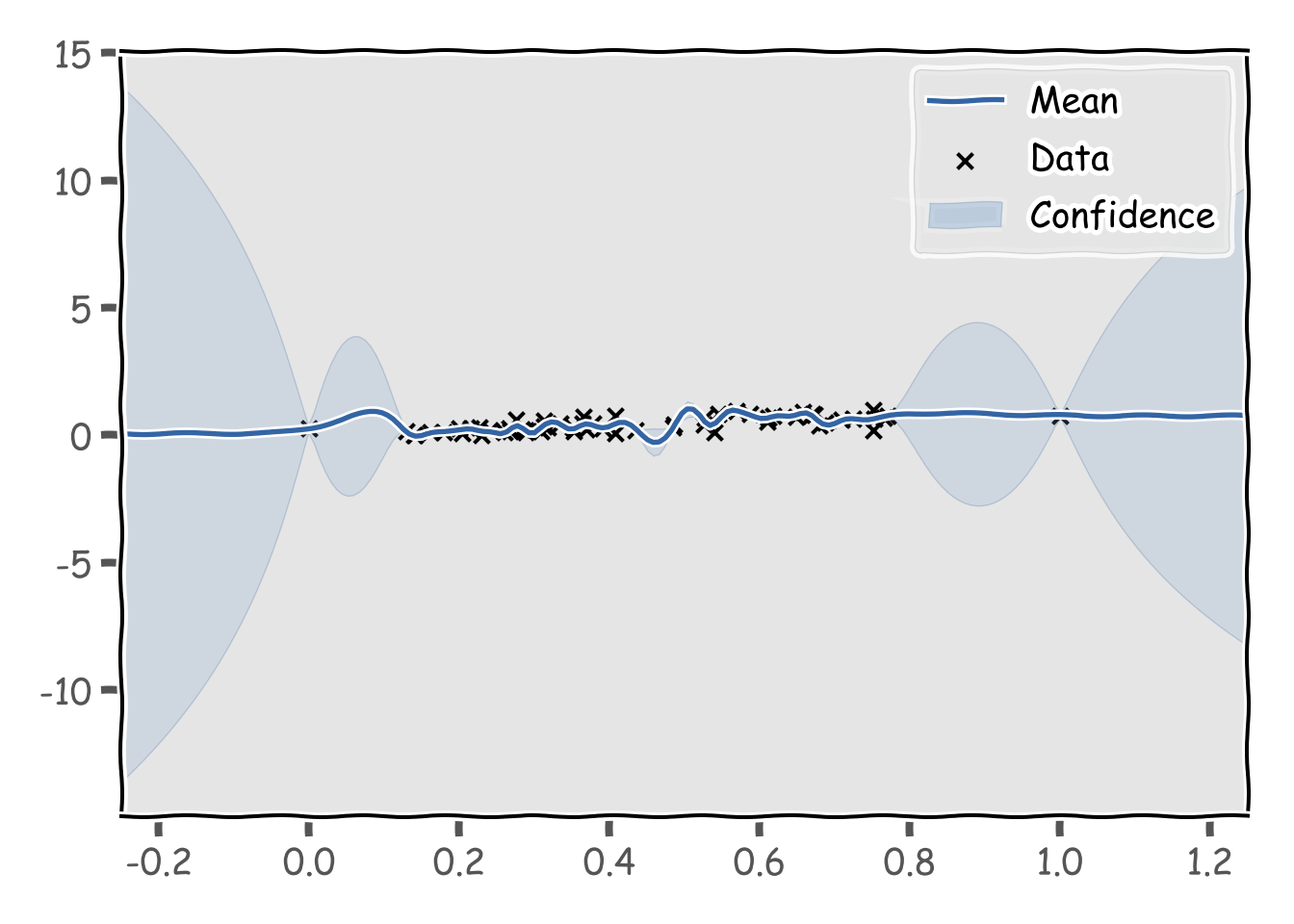
うーん、0-1以外の区間の信頼性はないかも。Student t processは過学習気味になることがわかりました。